DR-BART Implementation
variance = 'ux':
SCALE_MIX = TRUE
variance = 'x':
SCALE_MIX = FALSE
std::vector<vec_d> xinfo;
xi : cutpoints mean
xiprec : cutpoints prec
Each element in the vector represents a variable.
Each variable has cutpoints
di : data info
contains the x data and also the y datapinfo pi: Contains MCMC action probabilities
pbd : prob of birth / death
pd : prob of birth given birth / death
getpb : get probability of birth for a tree
returns 0 when there is no bottom node to split on
returns 1 when the tree is empty
else returns 0.5
Mean trees:
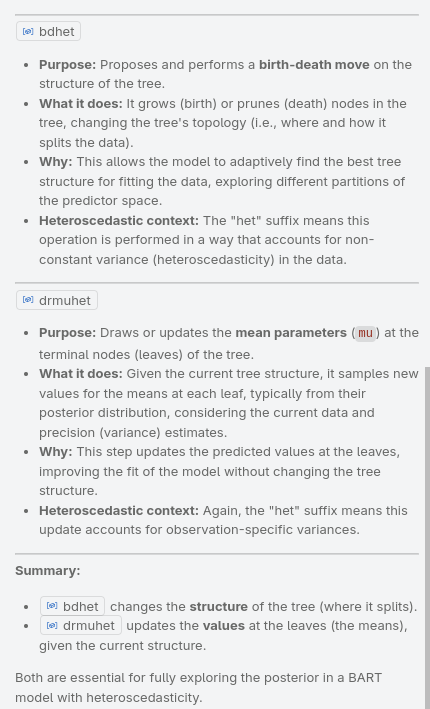
bdhet : birth-death heteroscedastic
- can change a mean tree by spawning / deleting new nodes
- First: Decide whether to birth or to death by using getpb
- if: birth operation; else: death operation
- For the birth operation:
- Randomly (uniformly distributed) samples a possible node to split on (from goodbots)
- Randomy (uniformly distributed) samples a possible variable to split on (from goodvars)
- Randomly (-||-) samples a cutting point from the variable
- Then calculates metropolis ratio: alpha
- Therefore calls: getsuffhet
- getsuffhet iterates over all samples to get [the numbers of samples for the two leaves (left and right) ???]
- and the likelihood?
- Therefore calls bn:
- Assumption: bn takes long when there are lots of u splits
- But getsuffhet it seems to ignore the other variables it has not split on?
- getsuffhet iterates over all samples to get [the numbers of samples for the two leaves (left and right) ???]
- If left or right samples < 5 : then do not birth, because the samples are too few
- Therefore calls: getsuffhet
- Then randomly samples probability (uniformly distributed): if it is smaller then alpha, then do the birth; else do not do it
- ...
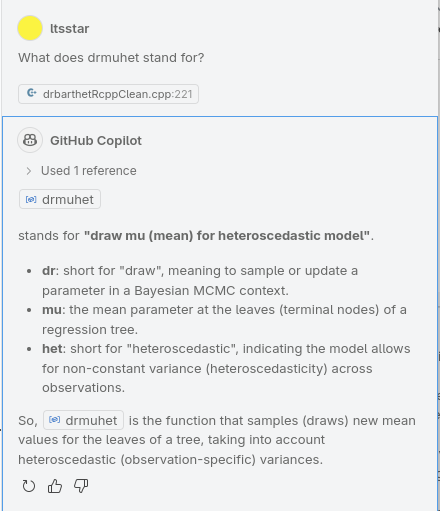
drmuhet : draw mu heteroscedastic (model)
- changes a mean tree t
- sets leave means to means of samples considering the variances(?)
Precision trees:
bdprec:
drphi:
- changes a precision tree
- updates leave precisions
- uses the gig_norm function. If I recall correctly, this is an approximation of the normal distribution and was mentioned in the paper


No Comments